на 2024/06/14 1,052

Текущи разделителни вериги и ефективно използване на формулата за разделител

Изследването на електрическите вериги, по -специално динамиката на разпределението на тока и напрежението при паралелни конфигурации, е крайъгълен камък на електротехниката и физиката.Тази статия изследва тънкостите на паралелните вериги, фокусирайки се върху основните принципи, които управляват разпределението на тока сред различните клонове.Чрез подробно изследване на текущото правило за разделител (CDR) и неговото сравнение с правилото за разделител на напрежението, тази дискусия осветява как инженерите и техниците използват тези принципи, за да проектират и анализират ефективно електрическите вериги.Използвайки математически модели, практически примери и теоретични рамки, статията се стреми да предостави цялостно разбиране за това как текущите се разделят на паралелни вериги и последиците от тези подразделения в практически приложения, от проектиране на по -безопасни електрически системи до оптимизиране на функционалността на веригата.

Каталог

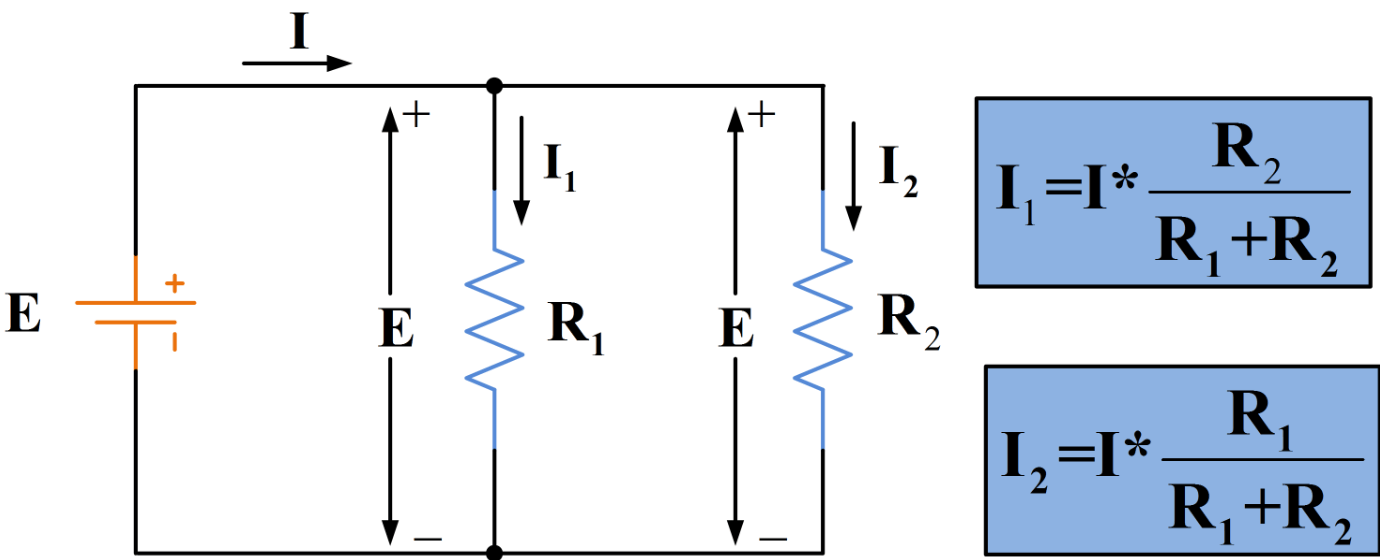
Фигура 1: Коефициенти на ток във вериги

Анализиране на съотношенията на тока в електрическите вериги

В паралелни вериги токът се разделя между различни клони въз основа на съпротивлението на всеки клон.Тази концепция прилича на разделители на напрежението, но вместо това се прилага за токове.Токът, преминаващ през всеки резистор във веригата, като R1 в сравнение с R3, поддържа фиксирано съотношение, дори ако напрежението на източника се променя.Например, ако токът през R1 винаги е два пъти по -голям от този на R3, това съотношение остава стабилно, независимо от колебанията в източника на напрежение.Това предсказуемо поведение се обяснява със закона на Ом, който гласи, че токът през резистор в паралелна верига е обратно пропорционален на неговата съпротивление.

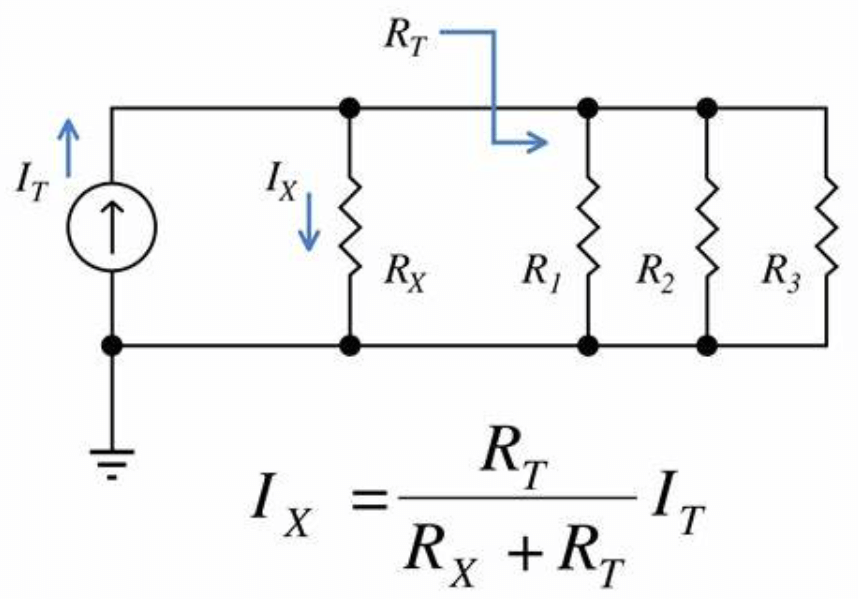
Паралелните вериги служат като текущи разделители, разделяйки общия ток от източника на части, които са обратно свързани с съпротивлението.Това може да се изразява математически като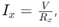
Къде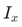е токът през резистора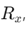и е постоянното напрежение във всички паралелни компоненти.Тази връзка показва, че текущото разделение в паралелна верига зависи не само от стойностите на съпротивлението, но и от принципа на опазването на тока, което диктува, че общият ток, влизащ в кръстовище, е равен на общия ток, който го оставя.

Фигура 2: Формула за разделител

Овладяване на текущата формула за разделител

Настоящата формула за разделител е основна концепция в електротехниката за анализ на токовите потоци в паралелни резистивни вериги.Той показва, че токът през всеки клон в паралелна верига е обратно пропорционален на съпротивлението на този клон, в сравнение с общото съпротивление на всички клони.Това помага да се опрости процеса на определяне на това как се разпределя токът между различни пътища във верига.

За да се изразява това количествено, токът през резистор в паралелна верига се изчислява, като се използва:

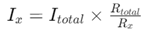
Тук, 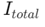е общият ток, който влиза в паралелната мрежа, 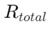е еквивалентното съпротивление на паралелната мрежа и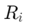представлява съпротивлението на всеки клон., Изчислен от:

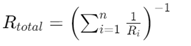
Тази формула е необходима за инженери и техници, защото им позволява да прогнозират тока във всеки клон на паралелна верига, без да измерват напрежението във всеки компонент.Освен опростяване на изчисленията, той помага за проектирането на вериги с желани токови характеристики.Тази оптимизация е динамична за подобряване на работата на системи като захранвания и осигуряване на безопасност, като се увери, че компонентите работят в текущите им граници.

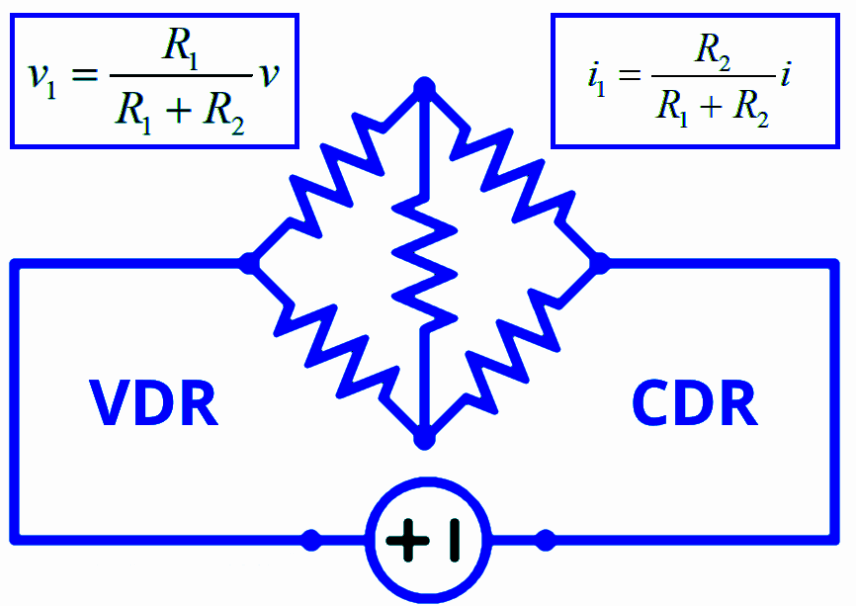
Фигура 3: Формули за разделител на разделител и напрежение

Сравняване на формулата за разделител на тока срещу разделител на напрежението

Разбирането на разликите и приликите между уравненията на напрежението и текущия разделител може да помогне за предотвратяване на грешки като неправилно прилагане на съотношенията на резистор.И двете формули разпределят общ вход (ток или напрежение) в компоненти въз основа на техните съпротивления, но те работят при различни условия и използват различни подходи за съпротивление.

Текущата формула за разделител се използва в паралелни вериги, за да се намери токът през определен клон.Той показва, че токът в клон е обратно пропорционален на неговата устойчивост в сравнение с общата паралелна устойчивост.Това означава, че клоните с по -ниска устойчивост ще носят по -висок дял от общия ток.Формулата на разделител на напрежението се прилага за серийни вериги и изчислява напрежението през определен компонент.Той показва, че напрежението през компонент е пропорционално на неговото съпротивление в сравнение с общата серия съпротивление.Следователно компонентите с по -висока съпротивление ще имат по -голям дял от общия спад на напрежението.

И двете формули създават съотношения на ключови, по -малко от една, подчертавайки функцията си като разделители.Те разделят вход (ток или напрежение) на по -малки, пропорционални части, а не увеличават стойностите.Идентифициране дали една верига е необходима или паралелна, е необходима за използване на правилната формула.Това разграничение определя как входът е разделен - текущ между паралелни пътища или напрежение по сериен път.

Проучване на използването на текущите разделители при електрическо измерване

Настоящите разделители са необходими в електрическите схеми, което позволява прецизно управление на потока на тока за точно измерване на електрическото използване.Тези вериги често изискват насочване на специфична част от тока чрез чувствителен инструмент, който се постига с помощта на резистор на шунт, изчислен с текущата формула на разделител.

Помислете за електрически метър, предназначен да измерва големи токове, с които стандартните инструменти не могат да се справят директно.Поставяйки резистор на шунт успоредно с измервателното устройство, текущата формула на разделител гарантира, че само безопасна, предварително определена фракция на тока тече през електромера.

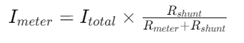
Изчисляването включва избора на стойността на резистора на шунт, която в комбинация с устойчивостта на измервателния уред, подходящо разделя тока.Тук, е общият ток,е съпротивлението на електромера и 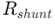е съпротивлението на резистора на шунта.Чрез внимателно избор 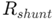, инженерите могат да контролират тока, който преминава през електромера, като гарантира, че той остава в безопасни оперативни граници, като същевременно предоставя точни данни за общо изчисления на потреблението на мощност.

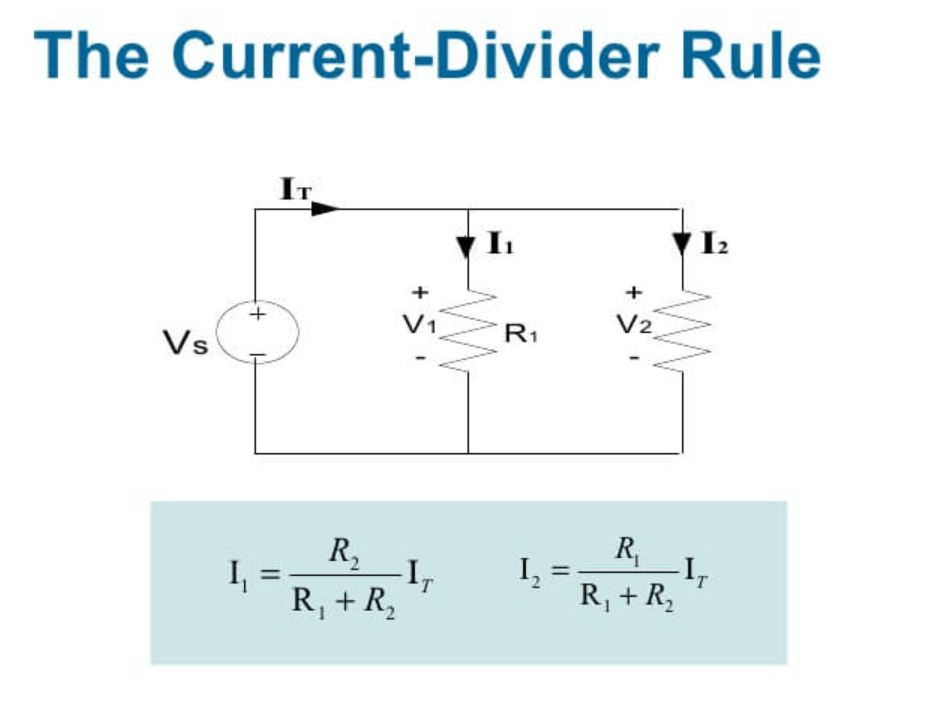
Фигура 4: Правило за текущи разделители

Подробни процедури за използване на текущото правило за разделител при изчисленията

Изчисляването на разпределението на тока в паралелни вериги, използвайки текущото правило за разделител (CDR), изисква систематичен подход, за да се гарантира точността и надеждността.

Стъпка 1: Проверете конфигурацията на веригата

Първо, потвърдете, че веригата е подредена паралелно.CDR се прилага само за паралелни вериги, където напрежението във всички компоненти е едно и също, но токовете могат да варират в зависимост от стойностите на съпротивлението.

Стъпка 2: Определете общия ток

След това идентифицирайте общия ток, влизащ в паралелната верига.Това може да бъде измерено директно от експериментални данни или да се получат с помощта на закона на Ом.Ако използвате закона на Ом, изчислете общия ток, като разделите общото напрежение на еквивалентното съпротивление на веригата.

Стъпка 3: Изчислете еквивалентно съпротивление

Изчислете общото съпротивление на паралелните клони.Това става чрез намиране на реципрочната сума на реципрочните съпротивления на всички индивидуални съпротивления: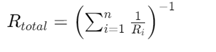

Стъпка 4: Изчислете тока за всеки клон

За всеки клон във веригата нанесете формулата CDR, за да определите отделните токов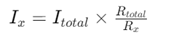е:Къде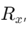е съпротивлението на анализа на клона.

Стъпка 5: Повторете за множество клони

Ако веригата има множество клони, повторете изчислението за всеки от тях.Уверете се, че всички съпротивления и токове се отчитат точно.

Стъпка 6: Проверете и валидирайте

И накрая, проверете изчисленията, като проверите дали сумата от токовете във всички клонове се равнява на общия ток, влизащ във веригата.Това се привежда в съответствие с принципа на опазване на тока.Освен това, потвърдете предполагаемите полярности и текущите посоки, за да предотвратите грешки при измерване или интерпретация.

Класифициране на перспективите за прилагане на текущото правило за разделител в дизайна на веригата

Настоящото правило за разделител (CDR) е необходимо за точно разпределение на тока в различни приложения за електротехника, играейки значителна роля в ефективния дизайн и управление на веригата.Той е особено ценен при работа с неравномерно натоварване в паралелни вериги, където осигурява прецизни прогнози за потока на тока във всеки клон.Това гарантира, че компонентите са правилно оценени и могат да се справят с техните специфични токове без риск от претоварване, което е сериозно във вериги с клони, които изпитват различни токови натоварвания.Освен това, CDR играе важна роля за контролиране на разсейването на мощността във вериги, където прегряването може да причини щети, подпомагайки стабилността и ефективността на приложения с висока мощност като захранващи блокове и системи за управление на двигателя.

CDR също има предимства в сложни вериги с множество клони.Тя дава възможност на инженерите да разберат как се разпределя ток по различни пътища, което е полезно за оптимизиране на оформлението на веригата и избор на подходящи компоненти.Това дълбоко прозрение помага да се гарантира, че всяка част от веригата работи в безопасни граници, необходимост по време на фазата на проектиране, поддръжката и отстраняването на неизправности.Като цяло способността на CDR да прогнозира и управлява токове допринася значително за надеждността и безопасността на електрическите системи.

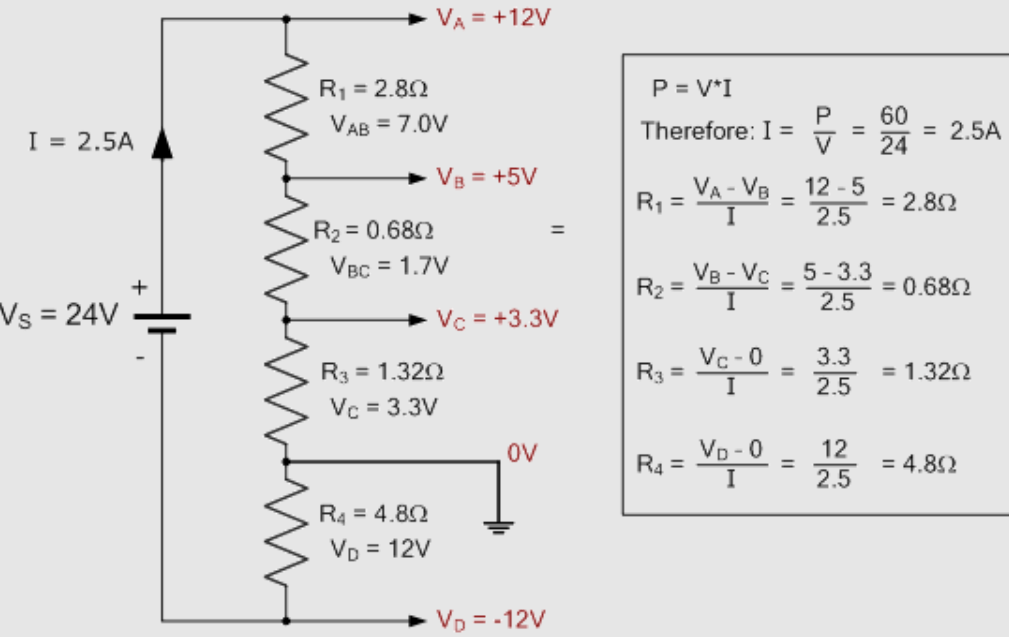
Фигура 5: Разделител на резистентен ток

Проектиране и функция на резистивните разделителни вериги

Разделителните вериги на резистивния ток са основни в електротехниката, илюстрирайки как токовете се разпределят в паралелни настройки.Тези схеми обикновено включват два или повече резистора паралелно, всяка от които получават част от общия входен ток, който след това се рекомбини в точката на връщане към източника.

Функционалност въз основа на законите на Kirchhoff и Ohm

Работата на резистивните текущи разделители разчита на сегашния закон на Кирчхоф, който гласи, че общият ток, влизащ в кръстовище, е равен на общия ток, който го оставя.Това гарантира, че сумата от токове през всеки паралелен път се равнява на първоначалния ток, влизащ във веригата.

Законът на Ом също е важен в тези схеми, осигурявайки метода за изчисляване на тока през всеки резистор.Тъй като напрежението във всички резистори в паралелна верига е постоянно, законът на Ом позволява лесно изчисляване на тока във всеки клон: 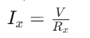КъдеV е напрежението през резисторите и R_x е съпротивлението на конкретен клон.

Резистивните схеми на разделителния ток са лесни примери за текущо разделение.На практика е необходимо да се анализира как да се контролират тези токове за проектиране на вериги, които изискват точни нива на ток чрез различни компоненти.Например, в системи, където различните компоненти се нуждаят от специфични нива на ток, за да функционират оптимално, резистивният ток разделител може да разпредели правилните токове въз основа на стойностите на съпротивлението.

Разбиране на текущото разделение чрез проводимост

Ефективен начин за анализ на текущите разделителни вериги е чрез използване на проводимост вместо съпротивление.Проводимост, реципрочната резистентност, опростява процеса на разбиране на разпределението на тока в паралелни резисторни вериги.

Проводимост в паралелни вериги

В паралелни вериги, изчисляването на общата проводимост е ясна.Общата проводимостG_общо е сумата от проводимостта на всеки паралелен резистор: 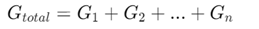Къде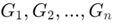са проводимостта на паралелните резистори.

Изчисляване на токове с помощта на проводимост

След като знаете общата проводимост, намирането на тока през всеки клон става по -лесно.Токът I_xВ клон с проводимостG_x се дава от:

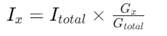
Тази формула позволява директно изчисляване на клоновите токове с помощта на проводимост, заобикаляйки необходимостта първо да се изчисли еквивалентно съпротивление и след това да се приложи традиционното правило за разделител на тока.

Използването на проводимост е особено полезно в сложни вериги, където изчисляването на индивидуални и общите съпротивления може да бъде досадно.Преобразуването на съпротивленията в проводимост опростява сумите, като прави токовите изчисления по -директни и намаляват потенциалните грешки.Приемането на проводимост за текущото разделение повишава гъвкавостта и ефективността на анализа на веригата.

Как да приложим текущото правило за разделител с помощта на проводимост

Използването на проводимост за прилагане на текущото правило за разделител осигурява по -ясен начин за анализ на токовия поток в паралелни вериги.Този метод се привежда в съответствие със свойствата на електрическата проводимост, предлагайки интуитивно разбиране на това как токовете се разпределят в различни клони.

В сравнение с традиционните методи, базирани на резистентност, използването на проводимост опростява изчисленията на текущото разпределение.При този подход проводимостта на всеки клон е в числителя, като подчертава, че по -високата проводимост (по -ниска съпротива) води до по -висок поток на тока.Токът през всеки клон в паралелна верига се дава от:

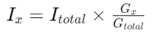
Тук,G_x е проводимостта на клона,G_общо е сумата от проводимостта на всички клонове иI_общо е общият ток, който влиза във веригата.Този метод, базиран на проводимост, осигурява по-ясна картина на потока на тока в вериги с множество паралелни пътища.Той е особено полезен в сложни системи, където стойностите на проводимостта директно измерват колко лесно тече тече през всеки компонент.

Основни случаи за използване на текущото правило за разделител

Текущото правило за разделител е ключов инструмент за анализ на потока на тока в сложни електрически вериги, особено в паралелни клони с множество резистори.Това правило е необходимо за определяне на отделните токове чрез всеки резистор, особено в сложни мрежи, където директното измерване е предизвикателно или непрактично.

Паралелен резистор: Това правило е специално проектирано за паралелни резисторни аранжировки.Например, във верига, в която резисторите R1 и R2 са паралелни, общият ток, влизащ в възела, споделен с R1 и R2, разделя между тях, обратно пропорционално на техните съпротивления.Това разделение опростява изчисляването на токовете във всеки клон, което прави анализа на веригата по -ефективен и надежден за различни приложения, от основна електроника до напреднали инженерни системи.

Изискване за равномерно напрежение: Ключово условие за прилагане на правилото за разделител на тока е едно и също напрежение във всеки паралелен клон.Това равномерно напрежение осигурява точни изчисления, като се приемат идентични нива на напрежение за всеки резистор.Ако има несъответствия в напрежението, модификации на вериги като източници на трансформации - конвертиране на източници на напрежение към еквивалентни източници на ток и обратно - може да се изисква да възстановят условията, подходящи за текущото правило за разделител.

Ограничение на линейните компоненти: Текущото правило за разделител работи само с линейни компоненти, които следват закона на Ом, което означава, че токът през компонент е пропорционален на напрежението през него и обратно пропорционално на неговото съпротивление.Това правило не се прилага за нелинейни елементи като диоди или транзистори, чието съпротивление варира в зависимост от приложеното напрежение.За схеми с такива елементи анализаторите се нуждаят от алтернативни методи, съобразени с нелинейни характеристики, като частично линеен анализ или специализиран софтуер за симулация.

Условие за стационарно състояние: Правилото за разделител на тока приема, че веригата е в стабилно състояние, където всички напрежения и токове остават постоянни с течение на времето.Това условие е значително, тъй като преходните явления - като включването или изключването на компоненти - могат да причинят временни колебания в ток или напрежение, потенциално изкривявайки анализа.При динамични условия по -модерните методи, като диференциално моделиране на уравнения или трансформации на Лаплас, са по -подходящи за улавяне и анализ на преходно поведение, осигурявайки подробно разбиране на времевата динамика на веригата.

Проучване на текущото правило за разделител при различни сценарии

Настоящото правило за разделител се използва широко в различни сценарии в реалния свят, вариращи от прости вериги с два резистора до сложни системи с множество резистори и източници на енергия.Тези примери показват как правилото гарантира ефективна и ефикасна работа на веригата.

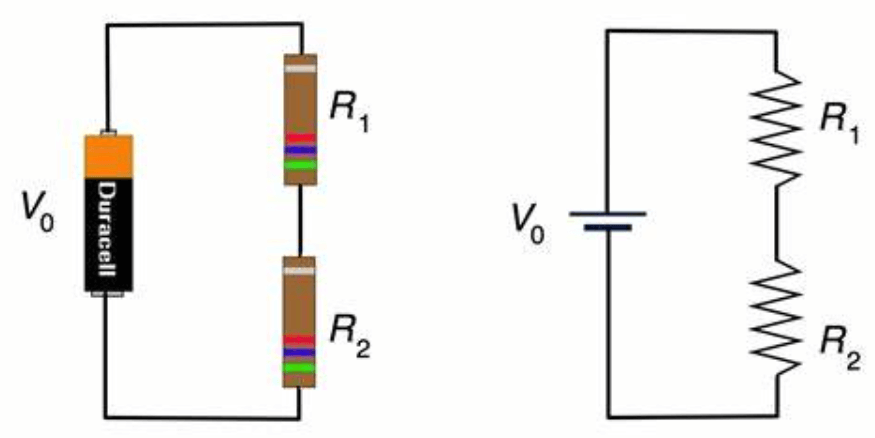
Фигура 6: Основна двурезисторна верига

Помислете за обикновена паралелна верига с общ ток от 10 ампера, течащи в възел и разделяне между два резистора,
Текущото правило за разделител изчислява тока през всеки резистор, както следва:

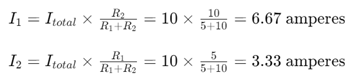
Този пример показва как токът е разделен пропорционално въз основа на стойностите на съпротивлението, като по -ниската съпротивление извлича по -ток.

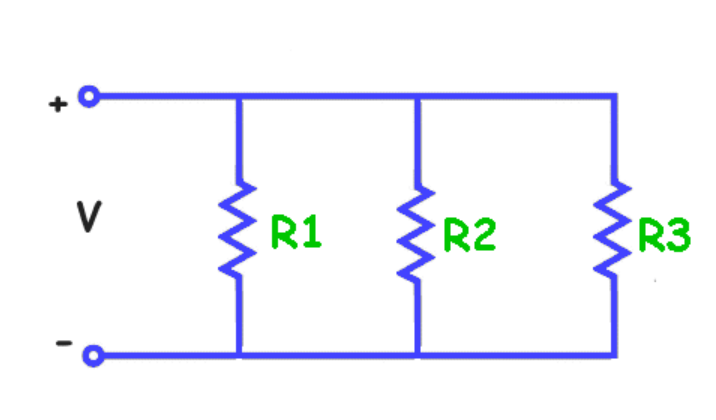
Фигура 7: Сложна многорезисторна верига

За по -сложен сценарий помислете за верига с множество резистори и общ ток от 15 ампера.Резисторите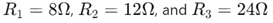
са свързани паралелно.Използване на текущото правило за разделител:

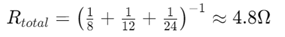
Токът през всеки резистор може да бъде намерен от:

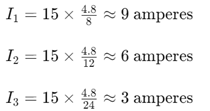
Това изчисление показва как различните съпротивления влияят на разпределението на тока.

Въздействието на текущите разделители в съвременните електронни системи

Настоящите разделители играят доминираща роля в различни приложения в рамките на електрониката и електротехниката.Те са необходими за функционалности, вариращи от пристрастия на компоненти до мониторинг на системата.

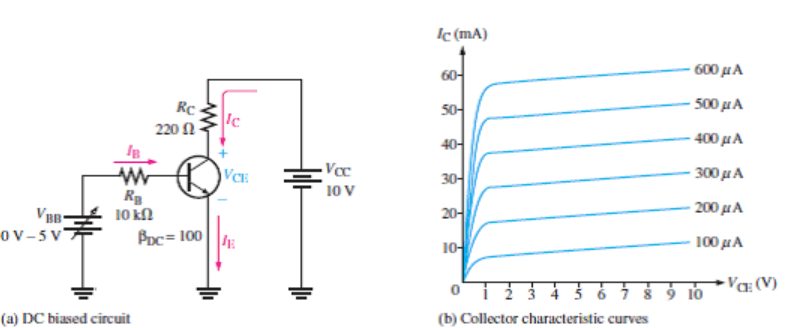
Фигура 8: Сменящи транзистори в електронни вериги

Текущите разделители са необходими за отклоняване на транзисторите.Чрез точно разделяне на тока, който се стича до базата на транзистора, те помагат да се определи операционната му точка в активния регион.Това гарантира стабилна производителност на усилвателя и ефективно превключване в цифрови схеми.

Фигура 9: Текущо разпределение на захранването

В веригите за захранване текущите разделители разпределят тока между различни компоненти безопасно и ефективно.Това предотвратява претоварването на компонентите и поддържа стабилни изходни напрежения при различни условия на натоварване, подобрявайки надеждността и ефективността на захранването.

Фигура 10: Текущи механизми за сензор

Настоящите разделители са категорични в текущите приложения за сензор.Те насочват управляемо количество ток чрез сензори, което е главно в среди с висок ток като системи за управление на двигателя.Измерването на малък, пропорционален ток точно позволява ефективен мониторинг и контрол на системата.

Фигура 11: Преобразуване на напрежение към ток

В процесите на преобразуване на напрежение към ток токът на разделителите регулират изходния ток въз основа на дадено входно напрежение.Това е ключово за взаимодействие между преобразувател, където сензорните сигнали трябва да бъдат преобразувани в ток за предаване на дълги разстояния, без да губят целостта на сигнала.

Фигура 12: Разпределяне на сигнали в електронни системи

Настоящите разделители също разпространяват сигнали в електронните системи, като гарантират, че сигналите се споделят между паралелни пътища с минимална загуба или изкривяване.

Заключение

Изследването на текущите съотношения и текущото правило за разделител в паралелни вериги изяснява основен аспект на електротехниката с далечни приложения.Разбирайки как се разпределя актуалният в различни клони въз основа на тяхната съпротива, инженерите могат да проектират схеми, които са едновременно ефективни и безопасни.Обсъжданите технически принципи, като законът на Ом и сегашното законодателство на Кирчхоф, не са само теоретични конструкции, но са ключови за практически приложения, като например при отклонение на транзисторите, проектирането на схеми за захранване и внедряването в текущите сензорни механизми.

Често задавани въпроси [FAQ]

1. Каква е формулата за текущия разделител на кондензатор?

В схема, съдържаща кондензатори, текущото правило за разделител се основава на импедансите (които зависят от честотата поради кондензаторите, които имат честота, зависима от честотата).Формулата за тока чрез кондензатор в паралелна мрежа е:

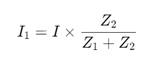
Къде Iе общият ток, който влиза в мрежатаZ_c е импедансът на кондензатора и Z_общое еквивалентният импеданс на паралелната мрежа.

2. Какво е разделител на напрежението и разделител на тока във верига?

Разделител на напрежението е схема, която извежда част от входното си напрежение през определен товар.Обикновено се състои от два резистора последователно, като изходното напрежение се приема в един от тях.

Текущият разделител е конфигурация, при която входящият ток се разделя на множество пътища във верига с различни клони, които имат своя импеданс.Разпределението на тока зависи от импеданса на всеки клон.

3. Какъв е математическият израз на текущата верига на разделител?

За основна верига на разделител с два клона с импедансиZ₁ и Z₂ токът презZ₁ се дава от:

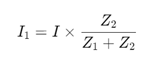
Тази формула се прилага за всеки пасивен компонент (резистори, кондензатори, индуктори), коригирайки импеданса по подходящ начин.

4. Как да разреша за ток?

За да решите за ток в схема, обикновено използвате закона на Ом,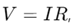
КъдеV е напрежението,I е токът и R е съпротивата.В по -сложни схеми може да използвате сегашния закон на Kirchhoff (KCL) и закона за напрежението на Kirchhoff (KVL), заедно със стойностите на импеданса за кондензатори и индуктори, ако присъстват.

5. Какво е правилото за напрежение и ток във верига?

Законът на Ом е основен за разбиране на взаимоотношенията в електрическите вериги, заявявайки, че токът през проводник между две точки е пряко пропорционален на напрежението през двете точки и обратно пропорционално на съпротивлението.

Настоящият закон на Kirchhoff (KCL) гласи, че общият ток, влизащ в кръстовище, трябва да е равен на общия ток, напускащ кръстовището.

Законът за напрежението на Kirchhoff (KVL) гласи, че сумата от разликите в електрическия потенциал около всяка затворена мрежа е нула.